闵可夫斯基和 / 差

闵科夫斯基和对应于图像处理中的膨胀操作(dilation)

闵可夫斯基差对应于图像处理中的腐蚀操作(erosion)

在几何中，闵可夫斯基和为两个位置向量的集合 $A$ 和 $B$，在欧式空间上进行两两相加的结果：

$A+B=\{\mathbf{a}+\mathbf{b} \mid \mathbf{a} \in A, \mathbf{b} \in B\}$

类似的，闵可夫斯基差的概念基于补集定义：

$A-B=\left(A^{c}+B\right)^{c}$

需要注意 $A-B \neq A+(-B)$。以一维上 $A = [-2, 2], B = [-1, 1]$ 为例：

$\begin{aligned} A-B = & \left(A^{c}+B\right)^{c} \\ = & \left([-2, 2]^{c}+[-1, 1]\right)^{c} \\ = & \left((-\infty, -2)\cup (2, \infty)+[-1, 1]\right)^{c} \\ = & \left((-\infty, -1)\cup (1, \infty)\right)^{c} \\ = & [-1, 1] \end{aligned}$

而 $A + (-B) = [-3, 3]$。

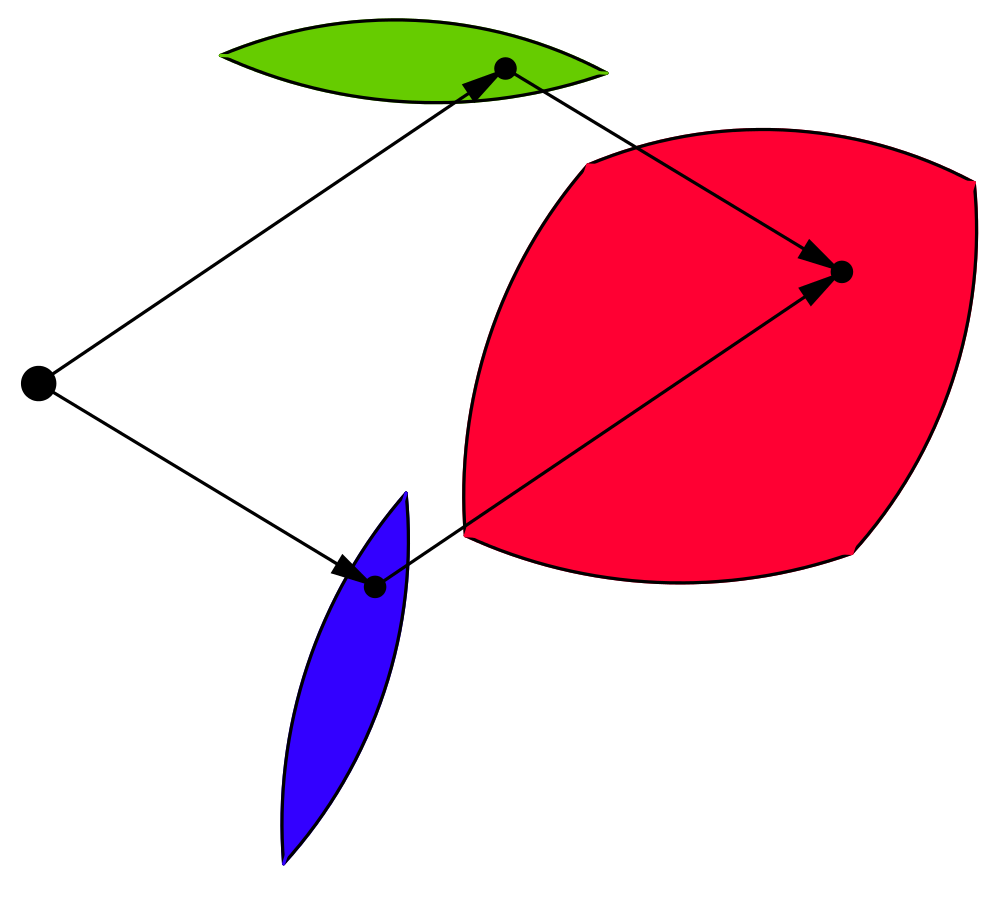
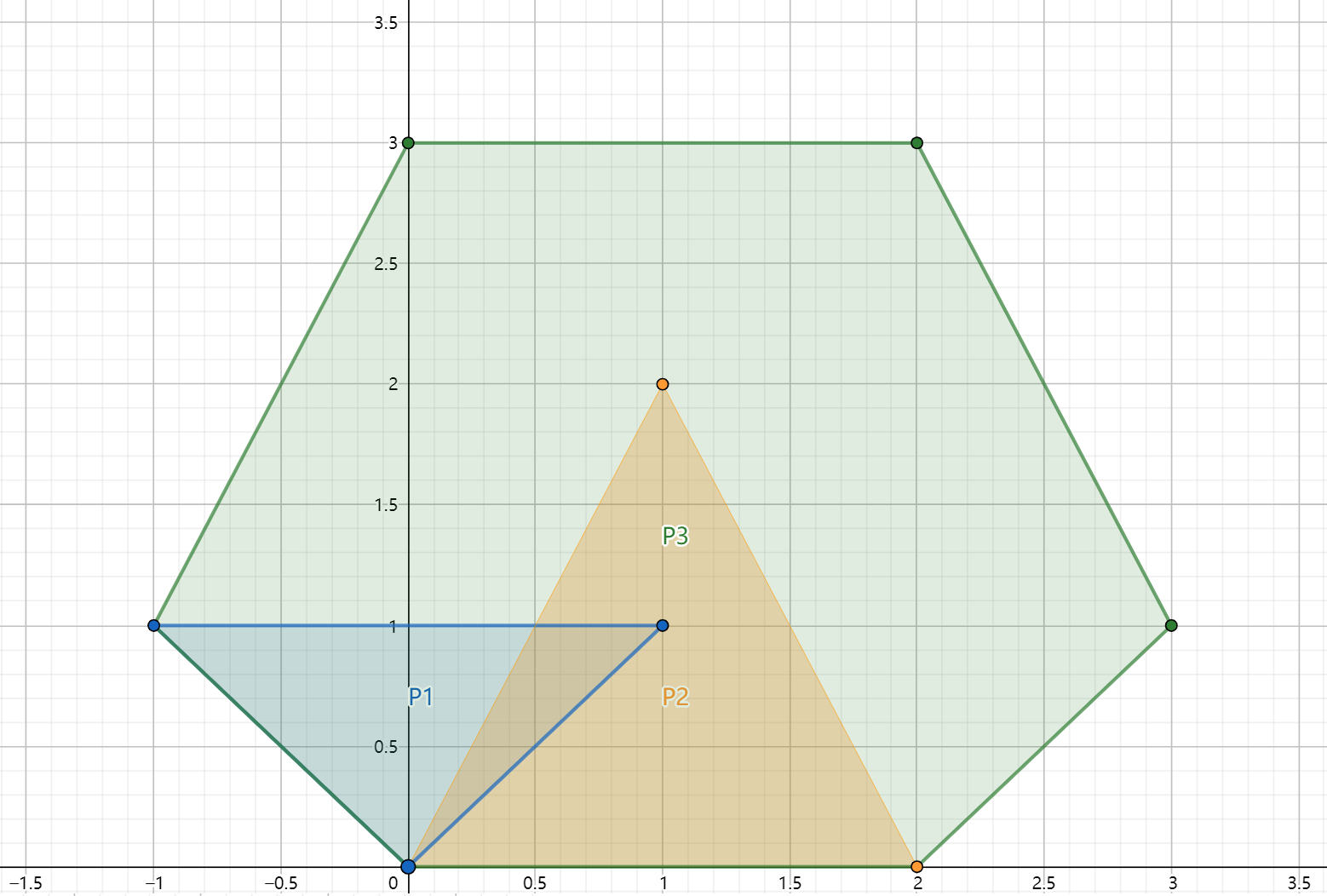
闵可夫斯基和求解

性质

若 $P$ 和 $Q$ 均为凸包，则 $P + Q$ 的结果为凸包

证明

设 $S = P + Q$ 中的点 $e, f \in S$，有 $a, b \in P, c, d \in Q$，且 $e = a + c, f = b + d$，则有：

$\begin{aligned} te + (1 - t) f = & t (a + c) + (1 - t) (b + d) \\ = & (ta + (1-t)b) + (tc + (1-t)d) \\ \in & P + Q \end{aligned}$

对于任意 $t \in [0, 1]$ 成立，因此 $P + Q$ 的结果为一凸包

$O(nm\log{nm})$ 复杂度解法

通过观察，$P$ 和 $Q$ 的闵可夫斯基和为 $P$ 和 $Q$ 中顶点依次两两相加结果的凸包。

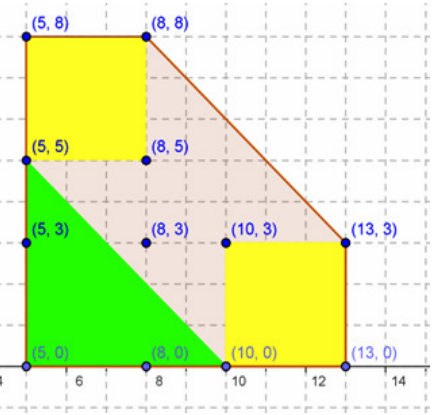
$O\left(n + m \log{\left( n + m \right) }\right)$ 复杂度解法

定理

对于凸包 $P$ 和 $Q$，$P + Q$ 的结果 $S$ 中的边，是由 $P$ 和 $Q$ 中的边按极角排序后连接的结果。

证明

将坐标系进行旋转，使得 $P$ 上的 $XY$ 与 $x$ 轴平行且在最下方，此时 $Q$ 中最低的点 $U$。

此时 $S$ 的最低靠左的点为 $A$，可知 $\overrightarrow{A} = \overrightarrow{X} + \overrightarrow{U}$。可知 $A$ 必然在 $S$ 的边界上。同理靠右侧点$\overrightarrow{B} = \overrightarrow{Y} + \overrightarrow{U}$。因此有 $\overrightarrow{AB} = \overrightarrow{XY} + \overrightarrow{U}$。

若按顺序进行如上的坐标系旋转，则结果连续地构成了 $S$ 中的每条边。

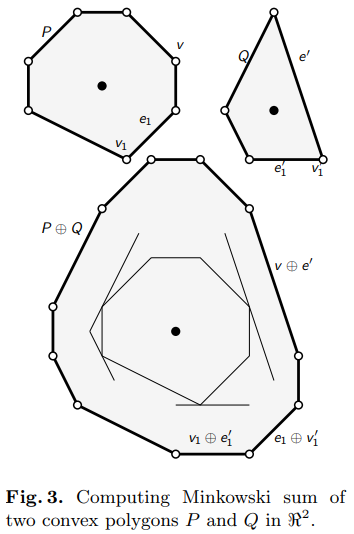
通过归并排序，能够在 $O(n + m)$ 时间复杂度内求得 $S$ 中的每条边。由于有三点同线的情形存在，可以通过再进行一次凸包运算解决。

多个凸包的闵可夫斯基和可直接将所有向量进行极角排序

模板

// BZOJ2564
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+5;
struct Point {
    ll x, y;
    Point(ll x=0, ll y=0) : x(x), y(y) {}
    Point operator - (const Point& rhs) const {
        return Point(x - rhs.x, y - rhs.y);
    }
    Point operator + (const Point& rhs) const {
        return Point(x + rhs.x, y + rhs.y);
    }
    ll operator ^ (const Point& rhs) const {
        return x * rhs.y - y * rhs.x;
    }
    bool operator < (const Point& rhs) const {
        return x == rhs.x? y < rhs.y: x < rhs.x;
    }
    bool operator == (const Point& rhs) const {
        return x == rhs.x && y == rhs.y;
    }
};
int n, m;
vector<Point> p1, p2;
Point stk[N];
int ConvexHull(vector<Point>& p) {
    sort(p.begin(), p.end());
    int tp = 0;
    stk[tp++] = p[0];
    for(int i = 1; i < p.size(); i++) {
        if(p[i] == p[i - 1]) continue;
        while(tp > 1 && ((stk[tp - 1] - stk[tp - 2]) ^ (p[i] - stk[tp - 2])) <= 0) tp--;
        stk[tp++] = p[i];
    }
    int m = tp;
    for(int i = p.size() - 2; i >= 0; i--) {
        if(p[i] == p[i + 1]) continue;
        while(tp > m && ((stk[tp - 1] - stk[tp - 2]) ^ (p[i] - stk[tp - 2])) <= 0) tp--;
        stk[tp++] = p[i];
    }
    p.clear();
    // for(int i = 0; i < tp - 1; i++) p.push_back(stk[i]);
    // 如果仅求凸包，应当把最后一个重复点去除
    // 此处因 Merge 合并需要用到每一条边，故保留重复点
    for(int i = 0; i < tp; i++) p.push_back(stk[i]);
    return tp;
}
vector<Point> Merge(vector<Point>& p1, vector<Point>& p2) {
    int tp = 0;
    stk[tp++] = p1[0] + p2[0];
    int i1 = 1, i2 = 1;
    while(i1 < p1.size() && i2 < p2.size()) {
        Point v1 = (p1[i1] + p2[i2 - 1]) - stk[tp - 1],
              v2 = (p1[i1 - 1] + p2[i2]) - stk[tp - 1];
        if((v1 ^ v2) >= 0) stk[tp++] = p1[i1++] + p2[i2 - 1];
        else stk[tp++] = p1[i1 - 1] + p2[i2++];
    }
    while(i1 < p1.size()) stk[tp++] = p1[i1++] + p2[p2.size() - 1];
    while(i2 < p2.size()) stk[tp++] = p2[i2++] + p1[p1.size() - 1];
    vector<Point> p;
    for(int i = 0; i < tp; i++) p.push_back(stk[i]);
    return p;
}
int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        ll x, y; cin >> x >> y;
        p1.push_back(Point(x, y));
    }
    for(int i = 1; i <= m; i++) {
        ll x, y; cin >> x >> y;
        p2.push_back(Point(x, y));
    }
    ConvexHull(p1);
    ConvexHull(p2);
    vector<Point> p = Merge(p1, p2);
    ConvexHull(p);
    ll ans = 0;
    for(int i = 1; i + 1 < p.size(); i++) 
        ans += (p[i] - p[0]) ^ (p[i + 1] - p[0]);
    cout << ans << endl;
    return 0;
}

闵可夫斯基和

闵可夫斯基和 / 差

闵可夫斯基和求解

性质

证明

$O(nm\log{nm})$ 复杂度解法

$O\left(n + m \log{\left( n + m \right) }\right)$ 复杂度解法

定理

证明

模板

题单

参考资料